Abstract

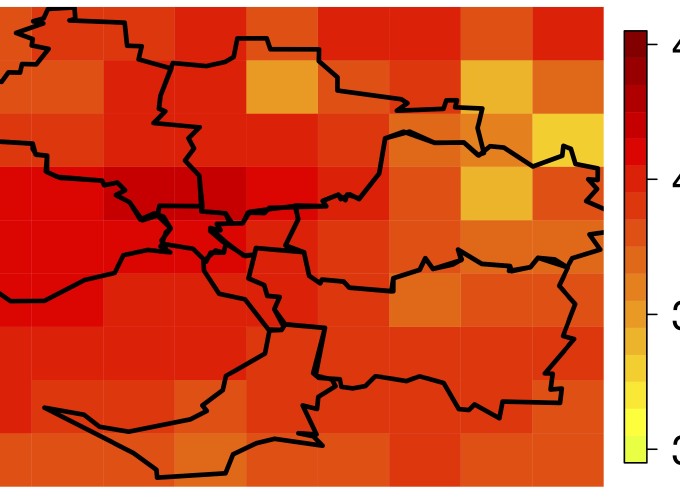
Max-stable processes are a popular tool to study environmental extremes and the extremal skew-t process is a general model that allows for a flexible extremal dependence structure. For inference on max-stable processes with high-dimensional data, full exact likelihood-based estimation is computationally intractable. Low-order composite likelihoods and Stephenson-Tawn likelihoods, when the times of occurrence of the maxima are recorded, are attractive methods to circumvent this issue. In this article we propose approximations to the full exact likelihood function, leading to large computational gains and enabling accurate fitting of models for 100-dimensional data in only a few minutes. By incorporating the Stephenson-Tawn concept ino the composite likelihood framework we observe greater statistical and computational efficiency for higher-order composite likelihoods. We compare 2-way (pairwise), 3-way (triplewise), 4-way, 5-way and 10-way composite likelihoods for models up to 100 dimensions. We also illustrate our methodology with an application to a 90 dimensional temperature dataset from Melbourne, Australia.