Extremal properties of the univariate extended skew-normal distribution, Part A
Jan 1, 2019· ,,,·
0 min read
,,,·
0 min read
Boris Béranger
Simone A. Padoan
Yangfan Xu
Scott A. Sisson
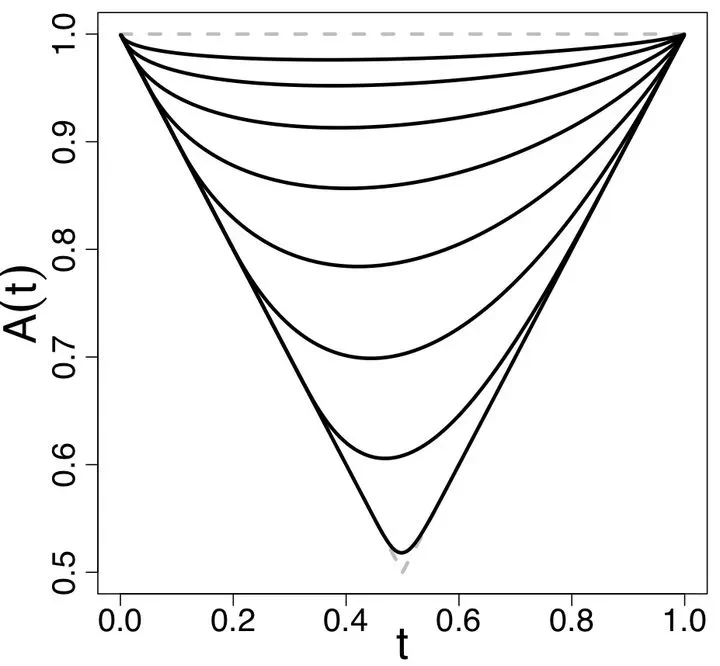 Figure 2
Figure 2Abstract
We consider the extremal properties of the highly flexible univariate extended skew-normal distribution. We derive the well-known Mills’ inequalities and Mills’ ratio for the extended skew-normal distribution and establish the asymptotic extreme-value distribution for the maximum of samples drawn from this distribution.
Type
Publication
Statistics and Probability Letters, 147, 73–82